It was the year of major changes in the academic programme of our junior school’s mixed age group classes. The environmental science curriculum took a renewed clarity in its intent, approach and content, which arose from the lush natural surroundings of the school with its incredibly rich biodiversity. The English curriculum shifted its emphasis from completing comprehension passages and filling up grammar worksheets to discerning the nuances of the language from a wide range of children’s literature. There was significant rethinking of the mathematics curriculum as well. A word of clarification here: while the curriculum as a sequence of steps including the fundamental mathematical operations necessarily remained the same, the look and feel of the mathematics classroom and the materials changed drastically, reflecting a fresh approach to the subject. Instead of focusing on procedures and algorithms as most of us have been trained to do in our childhood, we wanted children to understand the nuances of mathematics as a language with a historical evolution, with its own vocabulary and syntax that can provide a mathematical framework for comprehending the world. This article focuses on changes in one module of the mathematics curriculum —numbers and place value—to give an idea of how mathematics can be approached very differently from the textbook or conventional mode.

Along with language, in his essay On Proof and Progress in Mathematics, Thurston (1998) explains that the various facilities that help us in mathematical comprehension are vision, spatial sense, kinaesthetic sense, logic and deduction, intuition, association, metaphor, stimulus-response, and process and time. However, conventional maths education focuses heavily on stimulus-response, the procedural approach (‘if you see 3927 × 253, you write one number above the other and draw a line underneath’¹). We thus attempted to shift from this mainstream procedural approach to a more organic approach where the child’s lived experiences, real-life problem posing, and sometimes simply playing with numbers could become starting points for ‘thinking mathematically’.

Our lessons were so structured that the focus in the class was not on the booklets or written procedural work, but more on games, activities and story sessions, thus involving the verbal, kinaesthetic, visual, spatial, logical modes of being, and sometimes even including leaps of imagination, though in a mathematically guided manner! The vital role of stories in our maths curriculum needs to be highlighted here. Researchers and practitioners have discussed the importance of integrating literature and mathematics in the classroom because ‘children’s literature provides a context through which mathematical concepts, patterns, problem solving, and real-world contexts may be explored’². That is, a word problem becomes more meaningful if children are introduced to it through some appropriate story that provides a context for the underlying mathematical concept.

We used literature to provide a cultural and historical background to the concepts being learnt. As mathematicians and maths educators have often lamented, the subject of mathematics is usually taught in a dry and somewhat dead manner, where the formulae, definitions and theorems seem to be set in stone and given to us as final products. However, this very mathematics can instead provide a rich soil where the churning of thoughts and ideas of generations and cultures can be explored. As philosopher and educator John Dewey clarifies, ‘the various studies... embody the cumulative outcome of the efforts, the strivings, and the successes of the human race generation after generation’³ and children end up feeling disconnected from the curriculum when these human stories are forgotten in the classroom. Alternatively, if the curriculum can take off from the daily experiences of the child, or if the teacher can show the parallels between the child’s attempt to make sense of numbers and the historical development of numbers, an absorbing world of discovery and learning opens up. In Dewey’s words, ‘To interpret the child’s present crude impulses in counting, measuring, and arranging things in rhythmic series involves mathematical scholarship—a knowledge of the mathematical formulae and relations which have, in the history of the race, grown out of just such crude beginnings.’⁴

Consider, for example, the apparently simple yet profound concept of zero and the related decimal system of counting. To most children, zero is just a number that acts weirdly at times and does not seem to have any value of its own unless it is in some particular position in multiple digit numbers. They also know that if you had four marbles in your hand, and all of them fell down and rolled away, you are left with ‘nothing’ or ‘zero marbles’. Yet, as mathematicians and philosophers know, and as John Barrow encapsulates in The Book of Nothing, ‘Nothing, in its various guises, has been a subject of enduring fascination for millennia.’ Moreover, once the zero or mathematical nothing was invented, there followed ‘the development of universal counting systems that could evolve onwards and upwards to the esoteric realms of modern mathematics.’⁵

So what happens when this fascinating journey is brought into the classroom and how might one actually go about it? By delving into history, the idea of zero as a number and as a place-holder and the base-ten number system can be introduced to children over a couple of weeks of activities, stories and discussions, but in a way that is far removed from the typical textbook approach. Textbooks deal with numbers in terms of number sequences, what comes before/after/in-between, or with place value in terms of counting beads and bundles. Although such work is necessary, we need not be limited by these parameters. Instead, it is worthwhile to step back in time into a mathematically nascent world through open-ended questions such as ‘How would you count in a world where numbers (as we know them now) have not yet been invented?’

This halts even the mathematically proficient students in their tracks as they are encouraged to look deeper into the ideas behind numbers. The very suggestion that there could have been a world without numbers is intriguing. Children might suggest making marks or notches or knots. Once we brainstorm different ways to count objects and keep track of them—that is, record the information from the counting exercise—we need to find a way to communicate that information to someone else. Children can be prompted to come up with their own symbols for different numbers, and the seven-tonine- year-olds enjoy getting creative with the chalk. At this stage, their numerals are primarily pictorial. Next comes the challenge of remembering which symbol stands for which number and, in a world where the decimal zero has not yet been invented, they soon realize that for the number 15, you would need to invent and remember at least 15 different signs, and to reach any larger number—say 365—astonishingly, you would need those many symbols! Here are some of the numbers the children invented:

There can be a parallel or subsequent discussion that takes up a different strand, starting from tally marks. Kinaesthetically or intuitively, children can deduce that the reason behind counting tally marks in groups of five perhaps has something to do with the fact that we have five fingers in each hand; it is just a short step from there to counting in groups of tens. At this point, the usefulness and the probable origin of the base ten system of counting can be investigated through various hands-on activities, the ‘Shepherd and Boy counting activity’⁶ being a notable example.

Now the stage is set for the children to explore number systems in the ancient world. The ancient Egyptian base ten number system readily lends itself to the junior school age group. The system had different hieroglyphic numerals for each successive power of ten; the first three of them are shown below:

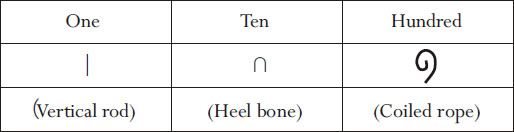
Different numbers were made by repeatedly using the necessary symbol(s). For example, three is │││ while thirteen is ∩│││. And,

Once the children know that there are different symbols for units, tens, hundreds and so on, they can also see the usefulness and advantage of this system over their invented numbers, since now they need remember only three different symbols to write any number below thousand. In playing with these numbers, the children soon realize that the position of the symbols do not matter in such a number system, since the symbol itself would tell them if it is a ten or a unit or a hundred. In fact, children have great fun coming up with different patterns or ways of writing the same number in the Egyptian system. For example, here is twenty-six written in three different ways :⁷

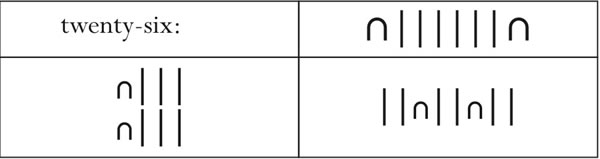
Furthermore, they also figure out that while only three symbols (one of each kind) are sufficient to show the number one hundred and eleven, things cease to remain as simple for all numbers. For example, to write the number nine hundred and ninety nine, you would need nine of each of the three kinds of symbols—in other words, the number would have twenty seven digits!⁸ We stumble upon the limitations of the Egyptian number system, where large numbers become cumbersome to write and work with.

Now what if we could have just a few symbols, but introduce the idea of positional or place value? Though in the Egyptian system, ││ is two, 11 in our system is not two but eleven. This is where we can discuss the significance of columns in our number system. Suddenly, the numbers we had taken so much for granted become so much more—and one begins to fully appreciate the simplicity and brilliance of our ten digit number system. While three ancient civilizations—Mayan, Babylonian and Indian—independently invented the zero, it was only in India that the zero played two significant roles. Firstly, it marked the absence of a number or acted as a place holder; secondly, it was a number by itself and was the answer in sums like 4 – 4 = 0. And with the zero around, we can write an infinite number of numbers using just ten numerals!

How was the zero invented? Did India just happen to be the place where zero was invented or is there an explanation behind it?⁹ Nina Shabnani’s animated film All About Nothing and the Tulika book of the same name sketch a possible historical origin of zero. This is one resource that I feel is a must-have in the maths class, as the story is not only thoroughly researched and well presented, but also touches upon the underlying philosophical framework in an accessible way. The Story of 1, a BBC documentary, is another resource that discusses the history of numbers. And books like Blockhead take off from where All About Nothing ends. Blockhead is about Fibonacci, who recommended the Indo-Arabic number system in the days when Europe was dominated by Roman numerals. Such resources bring alive for students the strivings, tensions, breakthroughs, cultural exchanges—in short, the genealogical development of ideas, and show how humans thought through problems before they could get to answers. The pressure of finding the ‘one right answer’ loosens its grip on us through such processes.¹⁰

French mathematician Laplace referred to the ‘grandeur of the achievement’ when he stated: ‘It is India that gave us the ingenious method of expressing all numbers by means of ten symbols’, and he considered it among the ‘first rank of useful inventions’.¹¹ Without being nationalistic or promoting a false sense of pride, I have sometimes found it useful to highlight the ‘Indianness’ of this invention, since it has the potential to challenge children’s unquestioned assumptions or conditioning of the modern world dominated by a Western world view. For instance, a student in my class firmly believed that zero and the decimal system had been invented by the Americans. When asked why he thought so, his answer was that the Americans have invented all the really important things!

When we start looking into the thinking behind mathematical concepts, children make connections, raise questions, come upon an insight. Once when we were discussing the importance of zero in class, a child wondered why we cannot jump from the number 9 straight to 11 and then again from 19 to 21 and so on, and thus make the zero irrelevant. A rich discussion followed as my students and I shared this insight. It is in moments such as these that we find sudden beauty in the subject, a beauty which often moves mathematicians and which eludes the students mired in algorithms. Winston Churchill says in his autobiography that his maths teacher helped him realize that ‘Mathematics was not a hopeless bog of nonsense, and that there were meanings and rhythms behind the comical hieroglyphics, and that [he] was not incapable of catching glimpses of some of these.’¹² From the teacher’s side, there is immense satisfaction in watching children trying to figure out a mathematical problem and finally getting that beaming smile when they have been able to come up with their own solutions. Bounded by procedures and computations, children soon come to dread the subject, but give them a glimpse into the fascinating world of thoughts and ideas and you will hear refrains of ‘I love maths!’ from the junior school children.

1 Thurston (1988, p. 343)
2 Moyer (2000, p. 246)
3 Dewey (2001, p. 109)
4 Dewey (2001, p. 113)
5 Barrow (2001, pp. xi-xii)
6 SMP (School Mathematics Project) booklet on numbers.
7 While position of the symbols did not matter, original hieroglyphs show that similar symbols were usually grouped together over multiple lines to facilitate the quick counting of the total number of symbols and thus enable quick reading of the number itself (as shown with the number ninety-nine above). Our students, however, were free to arrange the symbols in patterns of their own choice.
8 It is noteworthy that such a system of numbers whose absolute value is independent of position obviates the need for a zero.
9 The second question can be gone into more appropriately with an older age group. The philosophical connection is elucidated in Barrow.
10 In addition to the stories and activities discussed here, we also played games on number lines to learn about comparison. Children themselves became numbers and climbed up and down staircases for ascending and descending orders, learnt about uncountable numbers from stories like ‘How many stars’ (from Mathematwist: Number Tales from Around the World by T. V. Padma, Tulika Publications) or the poem ‘The Boy Who Counted Stars’ (by David Harrison), among other activities and games.
11 Laplace cited in Shumway, p. 80.
12 Churchill, p. 25

References:

Barrow, J. (2001). The Book of Nothing. London: Vintage Publications.
Churchill, W. (1958). My Early life: 1874–1904. NewY ork: Touchstone.
Dewey, J. (2001). The School and Society and The Child and the Curriculum.
Mineola, NY: Courier Dover Publications. (First published separately in 1899 and 1902 respectively)
Lockhart, P. (2009). A Mathematician’s Lament. New York: Bellevue Literary Press.
Moyer, P. (2000). ‘Communicating Mathematically: Children’s Literature as a Natural Connection’ in The Reading Teacher 54(3), pp. 246-255.
Shumway, J. (2011). Number Sense Routines: Building Numerical Literacy Every Day in Grades K-3. Portland: Stenhouse Publishers.
Thurston, W. (1998). ‘On Proof and Progress in Mathematics’ in Tymozcko ed. New Directions in the Philosophy of Mathematics. (Revised and enlarged edition). Princeton: Princeton University Press.